알파고(AlphaGo)가 이세돌 9단을 이겼다. (스코어 4:1)

도대체 인공지능이 뭐길래 컴퓨터가 인간의 자존심에 스크레치를 냈을까?

이번 포스트에서는 AlphaGo 를 개발한 DeepMind 사가 발표한 논문을 근거로 Artifitial Intelligence(인공지능) 기술을 이용한 AlphaGo 의 학습방법을 간략하게 소개합니다.

자세한 내용이 궁금하시면 아래의 논문을 참고하시기 바랍니다.

1. 논문 제목 : Mastering the game of Go with deep neural networks and tree search
2. 논문 출처
   • http://www.nature.com/nature/journal/v529/n7587/full/nature16961.html
   • 전문을 보시고 싶으시면 유료 결제를 해야 합니다.

이 논문의 내용을 제대로 이해하기 위해서는 인공지능에 관한 몇 가지 기반지식이 필요합니다.

• 확률, 통계
• Machine Learning
• Pattern Recognition
• Neural Network
• Deep Learning

하지만, 이런 내용을 모두 기술하기에는 내용이 너무 길어지므로 어느 정도 알고 있다는 가정하에 그때 그때 간략하게만 언급하고 넘어가도록 하겠습니다.

그리고, 논문에서 가장 중요하게 언급되는 용어가 policy network 과 value network 인데, policy network 은 다음에 놓을 수를 결정하는 정책에 관한 신경망이고 value network 는 어떤 수를 놓았을 때 승리할 확률에 관한 신경망이다. 다소 헷갈릴 수 있으므로 이를 염두에 두고 읽어야 한다.

Abstract

바둑 게임은 너무나 거대한 경우의 수와 계산량 때문에 인공지능으로 바둑 게임을 만드는 것은 다른 게임들에 비해 상당히 도전적인(어려운) 것으로 여겨왔습니다.

Deep neural networks 는 바둑 전문가들의 게임을 통한 지도학습(supervised learning)과 AlphaGo 스스로 플레이해 본 게임을 통한 강화학습(reinforcement learning)의 조합으로 훈련했습니다.

value networks 와 policy networks 라는 새로운 접근방법을 고안하였고, 이를 적용한 Monte Carlo tree search (MCTS) 알고리즘을 통하여 AlphaGo 는 다른 바둑 프로그램과의 게임에서 승률 99.8% 를 달성하였고 유럽 챔피언도 5:0 으로 꺾었습니다.

계산 복잡도

모든 게임에서 모든 플레이어가 최상의 플레이를 한다는 가정하에 최적의 승리 확률를 계산하는 함수를 $v^*(s)$ 라고 한다면,

계산복잡도는 $O(v^*(s)) = O(b^d)$ 이다.

• s : the current state : 게임의 현재 상태 (바둑이라면 19 x 19 의 바둑판에 돌이 놓여 있는 상태)
• b : the game’s breadth : 게임의 룰에 적합한 다음 수를 놓을 수 있는 모든 경우의 수 (바둑의 경우 : $b≈250$)
• d : the game’s depth : 게임의 승패가 결정날 때까지 남은 게임의 진행 턴 수 (바둑의 경우 : $d≈150$)

그런데, $250^150$ 개의 노드를 가진 트리를 모두 탐색한다는 건 절대 불가능한 일이다.

1초에 백만개의 노드를 탐색한다고 가정해도 아래 계산결과와 같이 너무나 오래 걸리기 때문이다. (단위 : years, 347 자리의 긴 수다. 혹시 양자 컴퓨팅 기술이 더 발전한다면 가능한 날이 올지도 모르겠다.^^)

$ bc
bc 1.06
Copyright 1991-1994, 1997, 1998, 2000 Free Software Foundation, Inc.
This is free software with ABSOLUTELY NO WARRANTY.
For details type `warranty'. 
(250^150)/(1000000*60*60*24*365)
15566633261344896477345801480803765991169506318174307347512522568452\
26171588570477061167517769321395318741619598278753967899517570530415\
68455337228060279155639684977944566905395070453164142481831503906327\
41648433536276002029426686960933536276002029426686960933536276002029\
42668696093353627600202942668696093353627600202942668696093353627600\
2029426

그렇다면, 계산복잡도를 줄이려면 어떻게 해야 할까? 당연히 $b^d$ 에서 b 와 d 를 줄이면 되겠다.

(이건 지금까지 연구된 거의 모든 인공지능 알고리즘의 공통점이다. 컴퓨팅 자원은 유한하므로 유한한 자원내에서 최적해에 근사한 수준에서 마무리할 수 밖에 없다.)

이 논문에서 제시한 방법도 마찬가지다.

다음 2가지 방법을 이용해 search tree의 depth 와 breadth 를 줄이기 위해서 neural networks(신경망)를 사용한다.

1. value network 를 이용해서 각 position 들을 평가함으로써 depth 를 줄이고,
2. policy network 를 이용해서 다음에 둘 수를 샘플링함으로써 breadth 를 줄인다.

다음 그림과 같이 여러 단계의 machine learning (기계 학습)을 이용해서 neural networks 를 훈련한다.

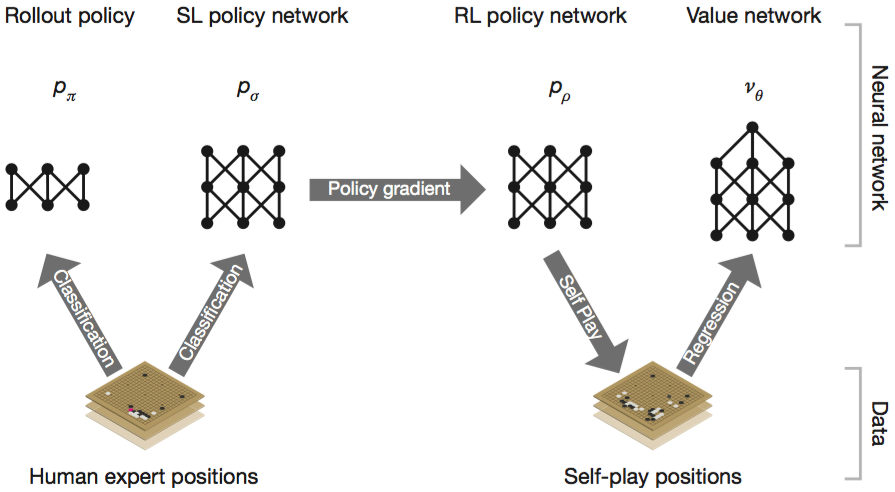
Supervised Learning of Policy Networks $P_σ$

첫 번째 단계로 SL Policy Network 는 전문가(KGS의 6단에서 9단 까지의 사람)들이 플레이한 160,000개의 대국 데이타를 기반으로 훈련을 시작한다.

이 과정에서 사람의 착수(현재 바둑판의 상태에서 다음 수를 놓는 것)에 대한 likelihood 를 최대화하기 위해서 gradient ascent 를 사용한다.

1. likelihood
   • 통계학 용어로 확률 분포의 모수가 어떤 확률변수의 표집값과 일관되는 정도를 나타내는 값
2. maximum likelihood
   • 모수가 주어졌을 때, 원하는 값들이 나올 likelihood 를 최대로 만드는 모수를 선택하는 방법
3. gradient ascent / gradient descent
   • gradient 는 기울기 또는 경사인데 이는 어떤 함수의 극대, 극소값을 빠르게 찾는데 이용할 수 있다.
   • 예를 들어, 등산을 할 때 정상으로 가는 가장 짧은 코스를 찾으려면 경사가 가장 큰 비탈면을 따라 올라가면 된다는 것이다.
   • 하지만, 치명적인 약점이 있으니 특이한 지형에서 길을 잃어 버리는 경우(산 중턱에서 기울기가 0인 평지를 만난다거나 정상보다 낮은 봉우리에 도달하는 경우)를 경계해야 한다. 이를 local optimization, local maximum 등의 다양한 용어로 부르고 있다.

$$ \Δσ = {α/m} ∑↙{k=1}↖m {∂ {log P_σ (a^k|s^k)} / {∂σ}} $$ $$\Δσ∝ {∂ log {P_σ (a|s)}} / ∂σ$$

저 같은 공돌이야 수식 한 줄이 더 편하지만, 그렇지 않은 분들을 위해 말로 풀어 쓰면…

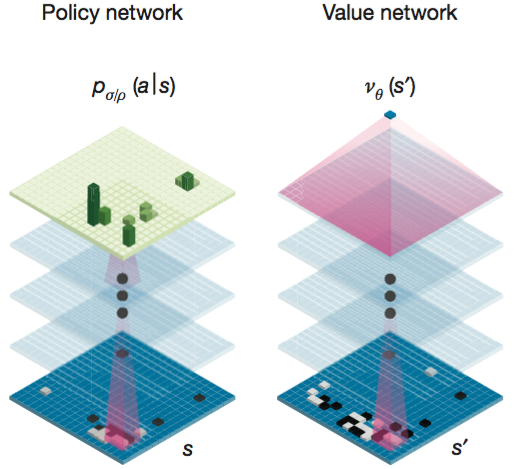
우선, policy network $P_σ(a|s)$ 는 현재 바둑판의 상태 s가 주어졌을 때, 다음 착수를 하는 행위 a 에 대한 확률을 학습하여 저장해 둔 정보이다. 전문가들의 약 3천만건의 기보정보를 바탕으로 학습한 확률이므로 전문가들이 많이 두는 자리는 확률이 높게 그렇지 않은 자리는 확률이 낮게 훈련된다. 다시 말해 policy network 는 전문가들의 대국을 흉내내기 위한 정보인 것이다.

그런데, 학습해야 할 기보정보가 방대하므로 $P_σ(a|s)$ 의 최대값을 빠르게 구하기 위해서 위에 언급한 gradient ascent 를 이용한다. gradient 를 구하는 수식이 위에 기술한 $\Δσ$ 를 표현한 식이다.

Reinforcement Learning of Policy Networks $p_ρ$

두 번째 단계에서는 policy network 를 개선하기 위해서 Reinforcement Learning(강화학습)을 진행한다. SL policy Network 을 시작으로 AlphaGo 프로그램이 스스로 백돌과 흙돌을 둘 다 쥐고 self-play 를 반복한다. self-play 의 승패 결과에 RL policy network 를 만들고 이를 기반으로 다시 학습을 반복하여 RL policy network 를 개선해 나간다. 이러한 학습 방법을 Reinforcement Learning (강화학습 혹은 증강학습) 이라고 한다.

$$\Δρ = {α/n} ∑↙{i=1}↖n ∑↙{t=1}↖{T^i} {∂ {log P_ρ ({a_t}^i|{s_t}^i)} / {∂ρ}} ({z_t}^i - v({s_t}^i))$$ $$\Δρ∝ {∂ log {P_ρ (a_t|s_t)}} / ∂ρ z_t$$

앞서 SL policy network 의 경우 대국결과를 이미 알고 있기 때문에 주어진 기보대로만 학습하면 되지만, RL policy network 의 경우 알파고가 self-play 를 통해 학습해야 하기 때문에 끝까지 시뮬레이션을 해봐야 대국 결과를 알 수 있다. 그래서 도입한 feature 가 위의 수식에 보이는 $z_t$ 이다.

$z_t = ± r(s_T)$

는 t 번째 턴에서 플레이어의 예상되는 대국 결과를 나타낸다. 끝까지(T 번째 턴) 뒀을 때, 이긴다면 +1, 진다면 -1 이다.

그런데, 여기에서 한 가지 놓친 부분이 있다. gradient ascent 를 설명하는 부분에서 Learning 과정에서 local optimization 을 경계해야 한다고 언급했었는데, 또 하나 주의해야 할 부분이 over fitting 을 경계해야 한다는 것이다.

RL policy network 는 self-play 를 반복하여 강화학습하는 과정이다. 자칫 current policy network 에 over fitting 될 수가 있다. 이러한 over fitting 을 막기 위해 이 논문에서는 policy network 의 previous iteration 을 랜덤하게 선택한다고 언급하고 있다. 다시 말해 self-play 를 반복하며 증강학습하는 과정에서 각 단계마다 여러 버전의 policy network 이 생성되는데 최신 policy network 만 사용하는게 아니라, self-play 시 한 쪽은 current policy network 로 다른 한 쪽은 이전 단계의 임의의 policy network 를 선택하여 서로 대국하도록 한다.

이렇게 해서 RL policy network 는 SL policy network 에 대해 승률 80% 를 달성했다고 한다.

Reinforcement Learning of Value Networks $v^p$

마지막 단계로 value network 를 훈련한다.

$$v_θ(s)≈v^{p_ρ}(s)≈v^*(s)$$

• $v^*(s)$ : 모든 플레이어가 최상의 플레이를 한다는 가정하에 최적의 승리 확률, 그러나 이는 계산 복잡도가 너무나 커서 실제로 계산하기 불가능하므로 policy network $p_ρ$ 를 사용하여 어림잡아 계산한다.
• $v^{p_ρ}(s)$ : policy network $p_ρ$ 를 이용한 승리 확률
• $v_θ(s)$ : RL policy network $p_ρ$ 의 value function 인 $v^{p_ρ}(s)$ 를 approximate 하기 위한 value network 을 따로 만들고 이를 이용한 승리 확률을 계산한다.

value network 은 policy network 와 유사한 구조를 갖는다. 다만, 어떤 수를 놓았을 때의 승리 확률에 대한 확률 분포가 아니라 승패 예측값 하나만을 결과로 내준다.

value network 는 1~450 사이의 값 U 를 랜덤하게 선택한 후, 다음 3단계를 거쳐 훈련한다.

1. 첫 번째 수 부터 U-1 번째 까지의 수를 SL policy network 을 통해 선택한다.
2. U 번째 수는 임의의 위치에 놓는다. (당연히 바둑 규칙에 부합하는 자리에 돌을 놓는다.)
3. U+1 번째 수 부터 게임이 끝날때 까지 RL policy network 을 통해 선택한다.

위 3단계를 모두 거쳐 게임이 끝나면 그 결과에 따라 z 값이 나오고 이러한 과정을 반복하여 각 게임마다 $(s_{U+1}, z_{U+1})$ 값의 pair 를 추출하여 이 데이타 셋을 value network 의 training set 으로 사용한다.

위에서 구한 (s, z) pair 에 대해서 회귀분석을 진행하여 value network 의 가중치 파라미터 $θ$ 를 훈련한다. 이때, 승패 예측 값 $v_θ(s)$ 와 실제 승패 결과 z 사이의 MSE(Mean Squared Error) 를 최소화하는 방향으로 진행하기 위해서 gradient descent 를 이용한다. 다음 수식이 $θ$ 에 대한 gradient 이다.

$$\Δθ = {α/m} ∑↙{k=1}↖m (z^k - v_θ(s^k)) {∂ v_θ(s^k)} / {∂θ}$$ $$\Δθ ∝ {∂ v_θ(s)} / {∂θ} (z - v_θ(s))$$

다음 그림은 policy network 과 value network 을 사용했을 때 게임이 진행될수록 실제 경기 결과와의 오차가 점점 줄어들고 있음을 보여준다.

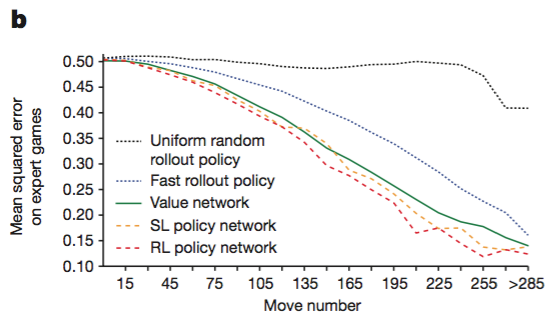
주목할 점은

1. SL policy network 이 상당히 좋은 예측값을 준다는 점
2. RL policy network 을 통해 SL policy network 보다 근소하게 성능이 개선된다는 점
3. value network 도 policy network 못지 않게 꽤나 좋은 성능을 보여준다는 점이 되겠다.

Searching with policy and value networks

AlphaGo 는 MCTS(Monte Carlo Tree Search) 알고리즘을 이용하여 policy network 과 value network 을 병합한다.

a. Selection

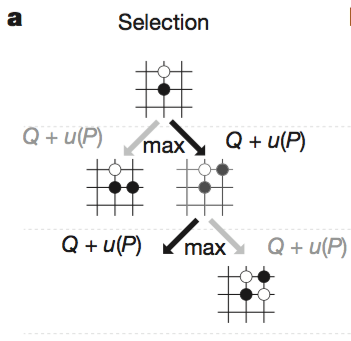
Tree 의 각 edge 는 $Q(s, a)$, $N(s, a)$, $P(s, a)$ 를 저장한다. 또한, root state(게임의 시작, 첫 수)부터 시작하여 각 step t(t 번째 수) 마다 다음 수식을 만족하는 action a 를 선택하면서 탐색한다.

$$a_t={argmax}↙{a} (Q(s_t, a) + u(S_t, a))$$ $$u(s,a)=c_{puct}{P(s,a)} {√{∑↙{b} N_r(s,b)}}/{1+N_r(s,a)}$$ $$u(s,a)∝{P(s,a)}/{1+N(s,a)}$$

• $Q(s,a)=1/{N(s,a)} ∑↙{i=1}↖{n} 1(s,a,i) V({s^i}_L)$ : action value
• $N(s,a)= ∑↙{i=1}↖{n} 1(s,a,i)$ : visit count
• $P(s, a) = p_σ(a∣s)$ : prior probability

위 수식에서 argmax 라는건 말 그대로 뒤 쪽 함수의 max 값을 갖는 arguments 를 의미합니다.

$u(s, a)$ 값이 뭔지 감이 잘 안 잡히시는 분들은 이 논문내의 그림보다는 위키피디아의 다음 그림에서 동그라미 속의 숫자를 참고하시면 이해가 쉬울 겁니다. (그런데, 위키피디아의 그림도 정확하지 않아서 제가 숫자를 약간 수정했습니다.)

b. Expansion

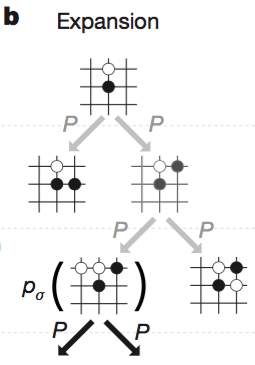
step L 에서 leaf node 에 다다르면, 그 leaf node 를 확장한다. 이때, SL policy network $p_σ$ 에 의한 확률값을 할당한다.

$$P(s, a) = p_σ(a∣s)$$

c. Evaluation

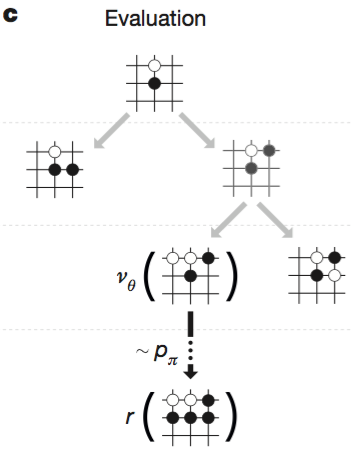
leaf node 는 다음 수식에 의해 평가된다.

$$V(s_L)=(1-λ)v_θ(s_L) + λz_L$$

• $v_θ(s_L)$ : value network 에 의한 value function
• $z_L$ : fast rollout policy $p_π$ 에 의 한 value function (승:+1, 패:-1)

rollout policy 란 tree 를 빠르게 탐색하기 위해서 여러가지 heuristic 에 기반한 패턴이라고 생각하면 되겠다.

d. Backup

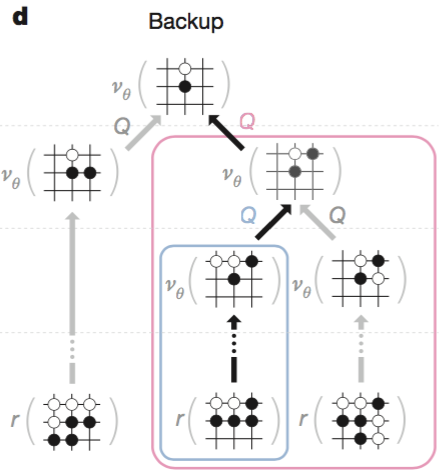
Selection -> Expansion -> Evaluation 과정이 모두 끝나면 각 node 에 필요한 값들을 업데이트한다. 이때 모든 노드들을 업데이트할 필요없이 새로운 leaf node 가 생긴 부분만 root 까지의 각 부모노드들을 따라 업데이트해 주면 되겠다. 이때 각 과정은 성능을 위해 비동기 방식 multi thread 를 사용하여 진행한다.

그런데, 여기에서 한 가지 내가 생각지 못한 부분이 있었다. Evaluation 까지 모두 끝난 노드들 중 승률이 가장 높은 노드를 선택하는게 아니라 가장 많이 방문한 노드(the most visited node)를 선택한다는 것이다.

생각해보니 RL policy network 이 SL policy network 보다 승률이 높다고 해서 모든 수에 대해 SL policy network 보다 좋으리라는 보장도 없고, value network 을 추가로 이용해서 승률이 높아지더라도 모든 수에 대해 더 좋으리라는 보장도 없다. 하물며 컴퓨터가 무수히 많은 계산을 통해 만들어낸 value function 보다 인간의 직관이 만들어낸 heuristic 이 더 좋은 수를 낼 수도 있다. 이러한 고민이 most visited node 를 선택한 배경이 아닌가 생각한다. 또한, 이것이 특정 신경망에 biased 되는 것을 경계하는 수단이 될 수도 있겠다는 생각이 든다.

SL policy network, RL policy network, Rollout, Heuristic 모든 것을 동원해 가장 유망한(threshold 보다 큰) 노드들을 점검한 후, 가장 많이 방문한 노드를 선택하는 것이 다양한 방법을 통해 검토해도 두루두루 비교적 유리한 수라는 결론에 이른 것이라 생각한다.

Evaluating the playing strength of AlphaGo

끝으로, AlphaGo 가 승률이 얼마나 좋은지를 자랑하는 섹션 되시겠다. 그냥 챠트를 보자.

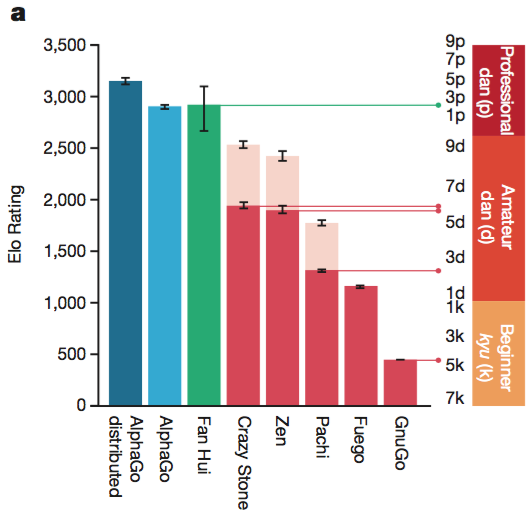
분산버전 AlphaGo 가 가장 강하다.

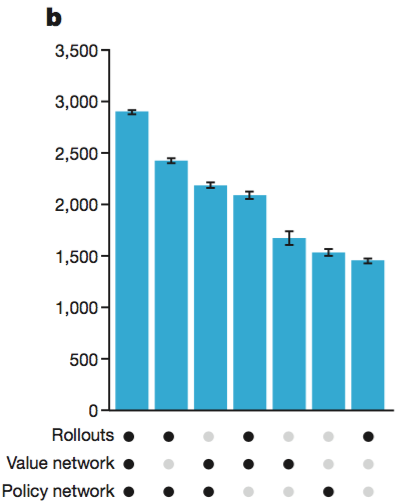
Rollouts, Value Network, Policy Network 을 모두 사용한 버전이 가장 강하다. 또한, 여기 그래프에는 표현되어 있지 않지만 rollout 과 value network 을 병합할 때 $λ=0.5$ 인 경우가 가장 성능이 좋다고 한다.

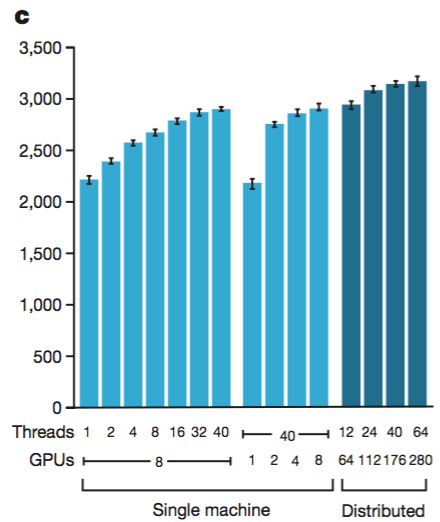
대체적으로 thread 를 많이 사용할수록, GPU 를 많이 사용할수록, 분산버전일수록 강하다. 하지만, 무작정 많이 사용한다고 linear 하게(선형적으로) 성능이 증가하는게 아니라서 최종 버전으로 40 search threads, 48 CPUs, 8 GPUs 정도로 사용하고, 분산버전은 40 search threads, 1,202 CPUs, 176 GPUs 를 사용한다고 한다.